Simetría rotacional
Publicado el 25 de marzo por David ‐ 7 min. de lectura
Objetivo: Establecer las herramientas para el análisis de la dinámica de un sistema de dos cuerpos.
Los elementos de la mecánica ondulatoria en tres dimensiones
El operador de posición 3D
El operador de posición en tres dimensiones se define mediante la ecuación de autovalor de espectro continuo dado por
$$ \hat{\boldsymbol{r}}|\boldsymbol{r}\rangle=\boldsymbol{r}|\boldsymbol{r}\rangle \Longleftrightarrow(\hat{x}, \hat{y}, \hat{z})|x, y, z\rangle=(x, y, z)|x, y, z\rangle $$
con las condiciones de ortogonalidad y completez dados por
$$ \begin{gathered} \left\langle\boldsymbol{r} \mid \boldsymbol{r}^{\prime}\right\rangle=\delta\left(\boldsymbol{r}-\boldsymbol{r}^{\prime}\right) \Longleftrightarrow\left\langle x, y, z \mid x^{\prime}, y^{\prime}, z^{\prime}\right\rangle=\delta\left(x-x^{\prime}\right) \delta\left(y-y^{\prime}\right) \delta\left(z-z^{\prime}\right) \\ \hat{1}=\int d \boldsymbol{r}|\boldsymbol{r}\rangle\left\langle\boldsymbol{r}\left|\Longleftrightarrow \hat{1}=\iiint d x d y d z\right| x, y, z\right\rangle\langle x, y, z| \end{gathered} $$
La ecuación de autovalor para el operador de posición y las condiciones de ortogonalidad y completez, en coordenadas esféricas, se describen como
$$ \begin{aligned} \hat{\boldsymbol{r}}|r, \theta, \phi\rangle & =r|r, \theta, \phi\rangle, \\ \left\langle r, \theta, \phi \mid r^{\prime}, \theta^{\prime}, \phi^{\prime}\right\rangle & =\delta\left(r-r^{\prime}\right) \delta\left(\theta-\theta^{\prime}\right) \delta\left(\phi-\phi^{\prime}\right), \\ \hat{1} & =\iiint r^{2} d r \operatorname{sen} \theta d \theta d \phi|r, \theta, \phi\rangle\langle r, \theta, \phi| . \end{aligned} $$
Hemos definido un sistema cuántico a través del vector de estado cuántico definido por el ket $|\alpha\rangle$, el operador de energía que mide el espectro discreto de energía posee un grado finito de autoestados de energía sobre el cual el vector de estado $|\alpha\rangle$ es expresado cuantitativamente como
$$ |\alpha\rangle=\hat{1}|\alpha\rangle=\sum_{i}\left|E_{i}\right\rangle\left\langle E_{i} \mid \alpha\right\rangle=\sum_{i} c_{i}\left|E_{i}\right\rangle $$
Aquí el vector de estado está descrito, cuantitativamente, como una combinación lineal de los autoestados de energía y esto proviene, estrictamente, de la condición de completez del espacio de Hilbert en que se define el operador de energía $\hat{H}$.
Si proyectamos el vector de estado sobre el espacio de posición obtenemos la función de onda
$$ \begin{aligned} \langle\boldsymbol{r} \mid \alpha\rangle & =\langle x, y, z \mid \alpha\rangle=\sum_{i} c_{i}\left\langle x, y, z \mid E_{i}\right\rangle=\sum_{i} c_{i} \Phi_{i}(x, y, z) \\ \Psi(\boldsymbol{r}) & =\Psi(x, y, z)=\sum_{i} c_{i} \Phi_{i}(x, y, z) \end{aligned} $$
esto implica que la función de onda es igual a una combinación lineal de autofunciones de energía del sistema cuántico donde los coeficientes son las amplitudes de probabilidad.
Las autofunciones de energía son los volúmenes (3D), áreas (2D) o longitudes (1D) que ocupan las partículas cuánticas al estar en un autoestado de energía $i$, y $c_{i}$ es la amplitud de probabilidad de que el sistema cuántico esté ocupando el autoestado $i$.
Por otro lado, la métrica del espacio de Hilbert para la mecánica cuántica afirma que
$$ \begin{aligned} 1 & =\langle\alpha \mid \alpha\rangle=\langle\alpha|\hat{1}| \alpha\rangle \\ & =\int d \boldsymbol{r}\langle\alpha \mid \boldsymbol{r}\rangle\langle\boldsymbol{r} \mid \alpha\rangle=\int d \boldsymbol{r} \Psi^{*}(\boldsymbol{r}) \Psi(\boldsymbol{r}) \\ & =\sum_{i} c^{*}_{i} c_{i} \int d \boldsymbol{r} \Phi^{*}_{i}(\boldsymbol{r}) \Phi_{i}(\boldsymbol{r})=\sum_{i}\left|c_{i}\right|^{2} \int d \boldsymbol{r}\left|\Phi_{i}(\boldsymbol{r})\right|^{2} \\ & =\sum_{i}\left|c_{i}\right|^{2} \int d \boldsymbol{r} \rho_{i}(\boldsymbol{r}) \end{aligned} $$
donde,
$\Psi(\boldsymbol{r})=\langle\boldsymbol{r} \mid \alpha\rangle=\sum_{i} c_{i} \Phi_{i}(\boldsymbol{r}) \quad$ y $\quad \Psi^{*}(\boldsymbol{r})=\langle\alpha \mid \boldsymbol{r}\rangle=\sum_{i} c_{i}^{*} \Phi_{i}^{*}(\boldsymbol{r})$
Para analizar la dinámica espacial de un sistema cuántico definimos el ope- rador de traslación en las tres dimensiones, en coordenadas cartesianas, como
$$ \begin{aligned} \hat{T}\left(a_{x} \mathbf{i}\right)|x, y, z\rangle & =\left|x+a_{x}, y, z\right\rangle \\ \hat{T}\left(a_{y} \mathbf{j}\right)|x, y, z\rangle & =\left|x, y+a_{y}, z\right\rangle \\ \hat{T}\left(a_{z} \mathbf{k}\right)|x, y, z\rangle & =\left|x, y, z+a_{z}\right\rangle \end{aligned} $$
o en términos vectoriales
$$ \hat{T}(\boldsymbol{a})|\boldsymbol{r}\rangle=|\boldsymbol{r}+\boldsymbol{a}\rangle $$
Los operadores que generan a los operadores de traslación son los operadores de momento lineal, que se expresan, analíticamente, de la forma siguiente
$$ \begin{array}{r} \hat{T}\left(a_{x} \mathbf{i}\right)=\exp \left[-i \hat{p}_{x} a_{x} / \hbar\right] \\ \hat{T}\left(a_{y} \mathbf{j}\right)=\exp \left[-i \hat{p}_{y} a_{y} / \hbar\right] \\ \hat{T}\left(a_{x} \mathbf{k}\right)=\exp \left[-i \hat{p}_{z} a_{z} / \hbar\right] \end{array} $$
A diferencia de los operadores de rotación, los cuales no conmutan cuando rotan en ángulos diferentes, los operadores de traslación sí conmutan cuando las traslaciones se realizan sobre direcciones diferentes,
$$ \hat{T}\left(a_{y} \mathbf{j}\right) \hat{T}\left(a_{x} \mathbf{i}\right)=\hat{T}\left(a_{x} \mathbf{i}\right) \hat{T}\left(a_{y} \mathbf{j}\right) . $$
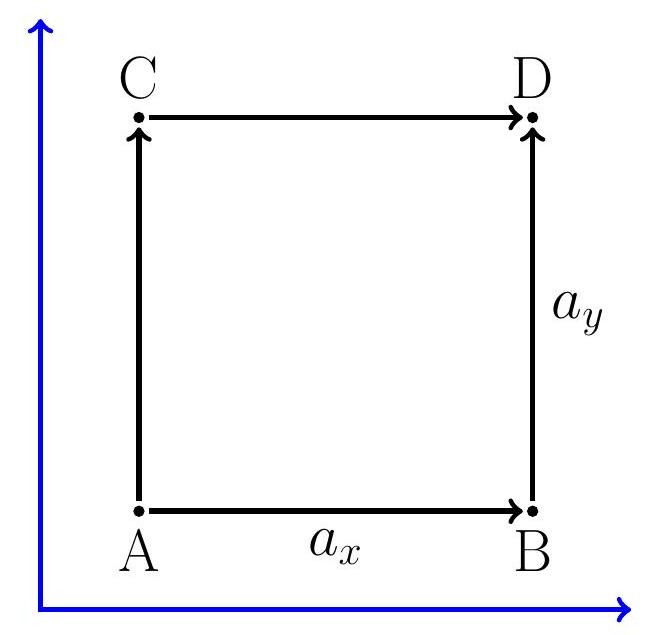
Probando la última expresión, hacemos
$$ \begin{aligned} & \hat{T}\left(a_{x} \mathbf{i}\right)=\exp \left[-i \hat{p}_{x} a_{x} / \hbar\right]=1-\frac{i}{\hbar} \hat{p}_{x} a_{x}+\left(\frac{i}{\hbar}\right)^{2} \hat{p}_{x}^{2} a_{x}^{2}-\ldots \\ & \hat{T}\left(a_{y} \mathbf{j}\right)=\exp \left[-i \hat{p}_{y} a_{y} / \hbar\right]=1-\frac{i}{\hbar} \hat{p}_{y} a_{y}+\left(\frac{i}{\hbar}\right)^{2} \hat{p}_{y}^{2} a_{y}^{2}-\ldots \end{aligned} $$
$$ \begin{aligned} \hat{T}\left(a_{x} \mathbf{i}\right) \hat{T}\left(a_{y} \mathbf{j}\right)&=\left(1-\frac{i}{\hbar} \hat{p}_{x} a_{x}+\frac{i^{2}}{\hbar^{2}} \hat{p}_{x}^{2} a_{x}^{2}-\ldots\right)\left(1-\frac{i}{\hbar} \hat{p}_{y} a_{y}+\frac{i^{2}}{\hbar^{2}} \hat{p}_{y}^{2} a_{y}^{2}-\ldots\right) \\ &=1-\frac{i}{\hbar}\left(\hat{p}_{x} a_{x}+\hat{p}_{y} a_{y}\right)+\frac{i^{2}}{\hbar^{2}}\left(\hat{p}_{x}^{2} a_{x}^{2}+\hat{p}_{y}^{2} a_{y}^{2}+\hat{p}_{x} \hat{p}_{y} a_{x} a_{y}\right)+\ldots \\ \hat{T}\left(a_{y} \mathbf{j}\right) \hat{T}\left(a_{x} \mathbf{i}\right)&=\left(1-\frac{i}{\hbar} \hat{p}_{y} a_{y}+\frac{i^{2}}{\hbar^{2}} \hat{p}_{y}^{2} a_{y}^{2}-\ldots\right)\left(1-\frac{i}{\hbar} \hat{p}_{x} a_{x}+\frac{i^{2}}{\hbar^{2}} \hat{p}_{x}^{2} a_{x}^{2}-\ldots\right) \\ &=1-\frac{i}{\hbar}\left(\hat{p}_{y} a_{y}+\hat{p}_{x} a_{x}\right)+\frac{i^{2}}{\hbar^{2}}\left(\hat{p}_{y}^{2} a_{y}^{2}+\hat{p}_{x}^{2} a_{x}^{2}+\hat{p}_{y} \hat{p}_{x} a_{y} a_{x}\right)+\ldots \end{aligned} $$
$$ \begin{aligned} \hat{T}\left(a_{x} \mathbf{i}\right) \hat{T}\left(a_{y} \mathbf{j}\right)-\hat{T}\left(a_{y} \mathbf{j}\right) \hat{T}\left(a_{x} \mathbf{i}\right)&=\frac{i^{2}}{\hbar^{2}}\left(\hat{p}_{x} \hat{p}_{y}-\hat{p}_{y} \hat{p}_{x}\right) a_{x} a_{y}=0 \end{aligned} $$
luego
$$ \hat{p}_{x} \hat{p}_{y}-\hat{p}_{y} \hat{p}_{x}=0 \Longleftrightarrow\left[\hat{p}_{x}, \hat{p}_{y}\right]=0 $$
Conclusión: El hecho de que los operadores de traslación conmutan cuando van en direcciones diferentes implica que los operadores generadores de la traslación en las diferentes direcciones, también conmutan.
El operador de traslación en forma vectorial está dado por
$$ \hat{T}(\boldsymbol{a})=\exp \left[-i \frac{\hat{\boldsymbol{p}} \cdot \boldsymbol{a}}{\hbar}\right] $$
El operador de momento lineal no conmuta con el operador de posición en las mismas direcciones
$$ \left[\hat{x}, \hat{p}_{x}\right]=i \hbar, \quad\left[\hat{y}, \hat{p}_{y}\right]=i \hbar, \quad\left[\hat{z}, \hat{p}_{z}\right]=i \hbar $$
pero el operador de traslación conmutan con el operador de posición en direcciones diferentes, veamos
$$ \begin{aligned} \hat{T}\left(a_{x} \mathbf{i}\right) \hat{y}|\alpha\rangle&=\hat{T}\left(a_{x} \mathbf{i}\right) \hat{y} \hat{1}|\alpha\rangle\\ & =\iiint d x d y d z \hat{T}\left(a_{x} \mathbf{i}\right) \hat{y}|x, y, z\rangle\langle x, y, z \mid \alpha\rangle \\ & = \iiint d x d y d z \hat{T}\left(a_{x} \mathbf{i}\right) y|x, y, z\rangle\langle x, y, z \mid \alpha\rangle\\ & = \iiint d x d y d z y\left|x+a_{x}, y, z\right\rangle\langle x, y, z \mid \alpha\rangle \\ & = \iiint d x d y d z \hat{y}\left|x+a_{x}, y, z\right\rangle\langle x, y, z \mid \alpha\rangle\\ & =\iiint d x d y d z \hat{y} \hat{T}\left(a_{x} \mathbf{i}\right)|x, y, z\rangle\langle x, y, z \mid \alpha\rangle \\ & = \hat{y} \hat{T}\left(a_{x} \mathbf{i}\right) \hat{1}|\alpha\rangle =\hat{y} \hat{T}\left(a_{x} \mathbf{i}\right)|\alpha\rangle \end{aligned} $$
Esto implica que
$$ \left[\hat{y}, \hat{T}\left(a_{x} \mathbf{i}\right)\right]=0 \Longleftrightarrow\left[\hat{y}, \hat{p}_{x}\right]=0 $$
De aquí deducimos que los operadores de posición y momento en las diferentes direcciones cumple
$$ \left[\hat{x}_{i}, \hat{p}_{j}\right]=i \hbar \delta_{i j} $$
El operador de momento lineal 3D
El operador de momento lineal es otro operador de espectro continuo que se define mediante la ecuación de autovalor de la siguiente forma
$$ \hat{\boldsymbol{p}}|\boldsymbol{p}\rangle=\boldsymbol{p}|\boldsymbol{p}\rangle \Longleftrightarrow\left(\hat{p}_{x}, \hat{p}_{y}, \hat{p}_{z}\right)\left|p_{x}, p_{y}, p_{z}\right\rangle=\left(p_{x}, p_{y}, p_{z}\right)\left|p_{x}, p_{y}, p_{z}\right\rangle $$
y las condiciones de ortogonalidad y completez dados por
$$ \left\langle\boldsymbol{p} \mid \boldsymbol{p}^{\prime}\right\rangle=\delta\left(\boldsymbol{p}-\boldsymbol{p}^{\prime}\right) \Longleftrightarrow\left\langle p_{x}, p_{y}, p_{z} \mid p_{x}^{\prime}, p_{y}^{\prime}, p_{z}^{\prime}\right\rangle=\delta\left(p_{x}-p_{x}^{\prime}\right) \delta\left(p_{y}-p_{y}^{\prime}\right) \delta\left(p_{z}-p_{z}^{\prime}\right) $$
y
$$ \hat{1}=\int d \boldsymbol{p}|\boldsymbol{p}\rangle\left\langle\boldsymbol{p}\left|\Longleftrightarrow \hat{1}=\iiint d p_{x} d p_{y} d p_{z}\right| p_{x}, p_{y}, p_{z}\right\rangle\left\langle p_{x}, p_{y}, p_{z}\right| $$
La ecuación de autovalor del operador de momento lineal y las condiciones de ortogonalidad y completez, en coordenadas esféricas, se expresan como
$$ \begin{aligned} \hat{\boldsymbol{p}}\left|p_{r}, \theta, \phi\right\rangle & =p_{r}\left|p_{r}, \theta, \phi\right\rangle \\ \delta\left(\boldsymbol{p}-\boldsymbol{p}^{\prime}\right) & =\delta\left(p_{r}-p_{r}^{\prime}\right) \delta\left(\theta-\theta^{\prime}\right) \delta\left(\phi-\phi^{\prime}\right) \\ \hat{1} & =\iiint p_{r}^{2} d p_{r} \operatorname{sen} \theta d \theta d \phi\left|p_{r}, \theta, \phi\right\rangle\left\langle p_{r}, \theta, \phi\right| \end{aligned} $$
El vector de estado que se describe en función de los grados de libertad del hamiltoniano se proyecta en el espacio de momento de la siguiente forma
$$ \begin{aligned} |\alpha\rangle=\hat{1}|\alpha\rangle & =\sum_{i}\left|E_{i}\right\rangle\left\langle E_{i} \mid \alpha\right\rangle=\sum_{i} c_{i}\left|E_{i}\right\rangle \\ \langle\boldsymbol{p} \mid \alpha\rangle & =\sum_{i} c_{i}\left\langle\boldsymbol{p} \mid E_{i}\right\rangle \\ \Psi(\boldsymbol{p}) & =\sum_{i} c_{i} \Phi_{i}(\boldsymbol{p}) \end{aligned} $$
donde $\Psi(\boldsymbol{p})=\langle\boldsymbol{p} \mid \alpha\rangle$ es la función de onda en el espacio de momento y $\Phi(\boldsymbol{p})=$ $\left\langle\boldsymbol{p} \mid E_{i}\right\rangle$ son las autofunciones de onda y $c_{i}$ son las amplitudes de probabilidad.
El operador de momento se ha definido de la forma
$$ \hat{p}_{x}=\frac{\hbar}{i} \frac{\partial}{\partial \hat{x}} \quad \hat{p}_{y}=\frac{\hbar}{i} \frac{\partial}{\partial \hat{y}} \quad \hat{p}_{z}=\frac{\hbar}{i} \frac{\partial}{\partial \hat{z}} \Longrightarrow \hat{\boldsymbol{p}}=\frac{\hbar}{i} \hat{\nabla} $$
de la misma forma el operador de posición está definido como
$$ \hat{x}=i \hbar \frac{\partial}{\partial \hat{p}_{x}} \quad \hat{y}=i \hbar \frac{\partial}{\partial \hat{p}_{y}} \quad \hat{z}=i \hbar \frac{\partial}{\partial \hat{p}_{z}} \Longrightarrow \hat{\boldsymbol{r}}=i \hbar \hat{\nabla}_{\hat{\boldsymbol{p}}} $$
De las ecuaciones, Ec. (37), encontramos la relación entre los autoestados de posición y los autoestados de momento,
$$ \begin{aligned} & \left\langle x \mid p_{x}\right\rangle=\frac{1}{\sqrt{2 \pi \hbar}} \exp \left[\frac{i}{\hbar} p_{x} x\right], \quad\left\langle y \mid p_{y}\right\rangle=\frac{1}{\sqrt{2 \pi \hbar}} \exp \left[\frac{i}{\hbar} p_{y} y\right] \\ & \left\langle z \mid p_{z}\right\rangle=\frac{1}{\sqrt{2 \pi \hbar}} \exp \left[\frac{i}{\hbar} p_{z} z\right] \Longrightarrow\langle\boldsymbol{r} \mid \boldsymbol{p}\rangle=\frac{1}{(2 \pi \hbar)^{3 / 2}} \exp \left[\frac{i}{\hbar} \boldsymbol{p} \cdot \boldsymbol{r}\right] . \end{aligned} $$
Relación entre las funciones de onda en el espacio de posición y de momento:
$$ \Psi(\boldsymbol{r})=\sum_{i} c_{i} \Phi_{i}(\boldsymbol{r}) \quad \wedge \quad \Psi(\boldsymbol{p})=\sum_{i} c_{i} \Phi(\boldsymbol{r}) $$
Por otro lado, la función de onda $\Psi(\boldsymbol{r})$ definida en el espacio de posición y de momento se desarrolla de la manera siguiente:
$$ \begin{aligned} \Psi(\boldsymbol{r})&=\langle\boldsymbol{r} \mid \alpha\rangle=\langle\boldsymbol{r}|\hat{1}| \alpha\rangle=\int d \boldsymbol{p}\langle\boldsymbol{r} \mid \boldsymbol{p}\rangle\langle\boldsymbol{p} \mid \alpha\rangle\\ & =\frac{1}{(2 \pi \hbar)^{3 / 2}} \int d \boldsymbol{p} \exp \left[\frac{i}{\hbar} \boldsymbol{p} \cdot \boldsymbol{r}\right] \Psi(\boldsymbol{p}) \\ \Psi(\boldsymbol{p})&=\langle\boldsymbol{p} \mid \alpha\rangle=\langle\boldsymbol{p}|\hat{1}| \alpha\rangle=\int d \boldsymbol{r}\langle\boldsymbol{p} \mid \boldsymbol{r}\rangle\langle\boldsymbol{r} \mid \alpha\rangle\\ & =\frac{1}{(2 \pi \hbar)^{3 / 2}} \int d \boldsymbol{r} \exp \left[-\frac{i}{\hbar} \boldsymbol{p} \cdot \boldsymbol{r}\right] \Psi(\boldsymbol{r}) \end{aligned} $$
A estas relaciones se les denomina las transformaciones de Fourier de las funciones de onda.